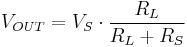Electrical load
If an electric circuit has a well-defined output terminal, the circuit connected to this terminal (or its input impedance) is the load. (The term 'load' may also refer to the power consumed by a circuit; that topic is not discussed here.)
Load affects the performance of circuits that output voltages or currents, such as sensors, voltage sources, and amplifiers. Mains power outlets provide an easy example: they supply power at constant voltage, with electrical appliances connected to the power circuit collectively making up the load. When a high-power appliance switches on, it dramatically reduces the load impedance.
If the load impedance is not very much higher than the power supply impedance, the voltage will drop. In a domestic environment, switching on a heating appliance may cause incandescent lights to dim noticeably.
A more technical approach
(Two sidenotes on generality, for advanced readers: This discussion assumes circuits are linear. It uses simple resistances, but can be readily generalized to impedances for AC analysis.)
When discussing the effect of load on a circuit, it is helpful to disregard the circuit's actual design and consider only the Thévenin equivalent. (The Norton equivalent could be used instead, with the same results.) The Thévenin equivalent of a circuit looks like this:
With no load (open-circuited terminals), all of 
falls across the output; the output voltage is . However, the circuit will behave differently if a load is added. We would like to ignore the details of the load circuit, as we did for the power supply, and represent it as simply as possible. If we use an input resistance to represent the load, the complete circuit looks like this:
Whereas the voltage source by itself was an open circuit, adding the load makes a closed circuit and allows current to flow. This current places a voltage drop across 
, so the voltage at the output terminal is no longer 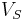. The output voltage can be determined by the voltage division rule:
If the source resistance is not negligibly small compared to the load impedance, the output voltage will fall.